Environment Map Importance Sampling
Environment maps are infinite light sources that can be represented as a sphere surrounding a 3d scene.
They supply incident radiance from all directions and can be sampled as a light source for 3d rendering. Since they can be created by real camera devices, you immediately get realistic results that create a rich visual complexity.
Though, environment maps are not always uniform; some areas may be a lot brighter compared to others. As a result, it is not obvious where important light sources to sample from are located and which directions should be prioritized when drawing direction samples in a path tracer.
In a Monte Carlo path tracer, samples are generated randomly and importance sampling is a technique in which we want to focus more of these random samples in areas where there is a larger contributions. This will effectively reduce the variance of the final result and converge faster.
If we were to generate random samples without importance sampling, we could miss out on smaller regions that may contribute significantly to the result (For example, imagine a very bright spot light that is far away from the viewer, chances of hitting it randomly would be low). With importance sampling, given that we're over representing and focusing on these regions of interest, we need to weight them less: this why we use a Probability Distribution Function (PDF) in Monte Carlo integration.
This post describes two things, first a minimal approach to finding areas of interest from an environment map, and the associated PDF used to sample these areas in a Monte Carlo integration.
Environment Map Binning
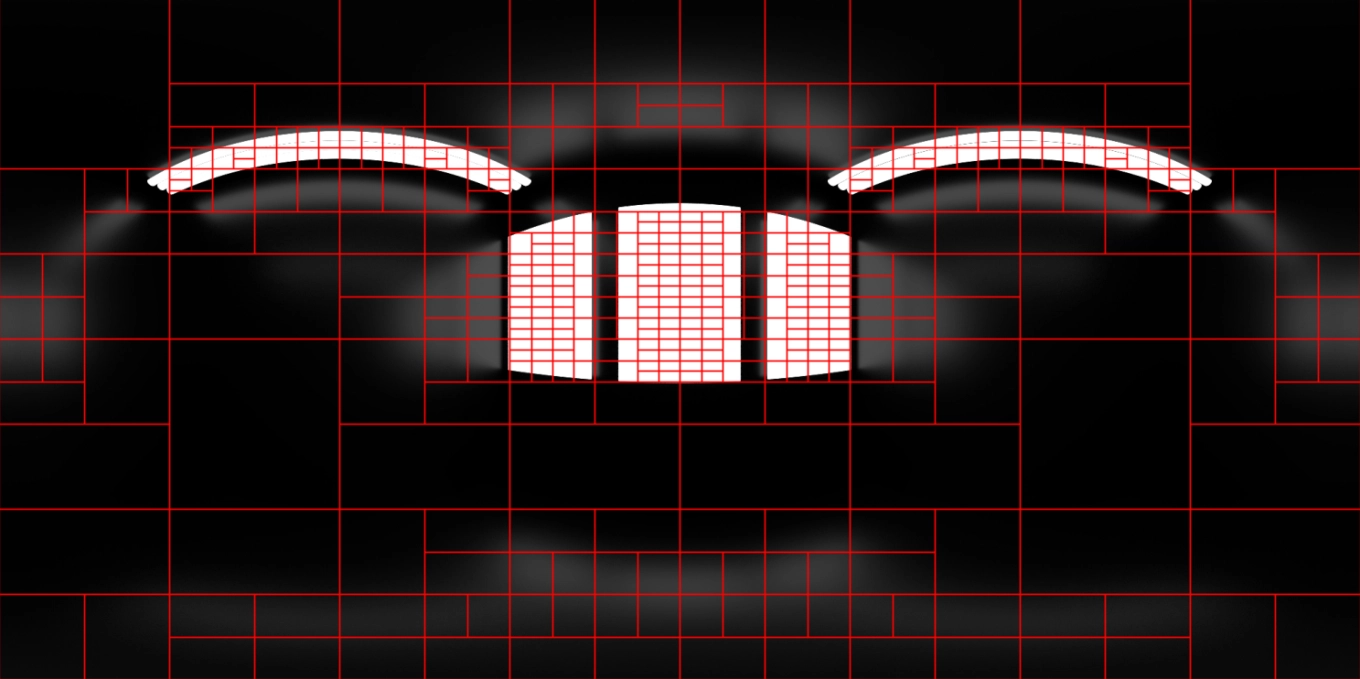
As we'd like to generate more samples where it matters the most (e.g. where light sources are in the environment map image), we need to find a way to increase the chances of hitting areas of high radiance.
The goal of the algorithm is to split the image in areas of equivalent radiance recursively. In other words, we create more areas where higher region of radiance are, and less where there are less important light sources. Later, during sampling, we will randomly select these areas and, as a result of having more areas around light sources, we will sample them more.
For an iteration of the split algorithm, we accumulate the radiance of the entire area and split on the largest axis. Then, we run a new iteration on each of the newly created areas from that split adjusting the appropriate amount of radiance for each of the new sections. We stop when either the area is too small or the amount of radiance of the area is below a given threshold.
def process_bins(bins, radiance_prev, x0, y0, x1, y1):
w = x1 - x0
h = y1 - y0
if (radiance_prev <= MIN_RADIANCE or w * h < SMALLEST_BIN_AREA):
bins.append([x0, y0, x1, y1])
return
# assign new bins based on largest axis
vertical_split = w > h
xsplit = w / 2.0 + x0 if vertical_split else x1
ysplit = y1 if vertical_split else h / 2.0 + y0
# accumulate the radiance for the current iteration
radiance_curr = 0.0
for x in range(x0, xsplit):
for y in range(y0, ysplit):
radiance_curr += radiance(x, y)
process_bins(bins, radiance_curr, x0, y0, xsplit, ysplit)
# substract the radiance and process the remainder
radiance_new = radiance_prev - radiance_curr
if vertical_split:
process_bins(bins, radiance_new, xsplit, y0, x1, y1)
else:
process_bins(bins, radiance_new, x0, ysplit, x1, y1)
Sampling and PDF

For sampling, the goal is to generate random variables from the environment map domain in polar coordinates $(\theta,\phi)$, convert them to a direction $(x, y, z)$ and find the random sample PDF function.
To sample a direction, we first randomly select a bin, then generate two random values from within that bin and finally convert it to a direction vector in Cartesian coordinates.
void EnvironmentMapSample(out vec3 sample_dir, out float pdf) {
float num_bins = float(NUM_BINS);
vec4 bin = vec4(u_environmentMapBins[num_bins * RandomFloat01()]);
float bin_width = bin.z - bin.x;
float bin_height = bin.w - bin.y;
// Generate a random sample from within the bin
vec2 uv = vec2(
bin_width * RandomFloat01() + bin.x,
bin_height * RandomFloat01() + bin.y);
uv /= u_environmentMapSize;
float phi = uv.x * 2.0 * PI;
float theta = uv.y * PI;
float sin_theta = sin(theta);
// Convert to cartesian coordinates
sample_dir = vec3(cos(phi) * sin_theta, sin(phi) * sin_theta, cos(theta));
float bin_area = bin_width * bin_height;
float bin_pdf = u_environmentMapArea / (num_bins * bin_area);
pdf = sin_theta == 0.0 ? 0.0 : bin_pdf / (2.0 * PI * PI * sin_theta);
}
To derive the PDF above, we start by defining a function $f$ that maps two $u$ and $v$ values to the domain $[0, 2\pi]$ x $[0, \pi]$: $f(u, v)=(\theta, \phi)=(2\pi u, \pi v)$.
Using the change of variable definition for joint PDF, we first need to calculate the Jacobian of $f$: $|J_{f}|=2\pi^2$. Applying the change of variable on the PDF we get:
$p(\theta, \phi)=p(f(u, v))=\frac{p(u, v)}{|J_{f}|}=\frac{p(u, v)}{2\pi^2}$
Then, we define a similar function $g(\theta, \phi)=(x, y, z)$ mapping values from polar coordinate to Cartesian. As $(x, y, z)=(sin(\theta)cos(\phi), sin(\theta)sin(\phi), cos(\theta))$, we have the Jacobian $|J_{g}|=sin(\theta)$ for the function $g$. Applying another change of variable on the PDF we have:
$p(x, y, z)=p(g(\theta, \phi))=\frac{p(\theta, \phi)}{|J_{g}|}=\frac{p(\theta, \phi)}{sin(\theta)}=\frac{p(u, v)}{sin(\theta)2\pi^2}$
We now need to define $p(u, v)$ based on the way the bins are sampled. We first generate a random variable to select a bin, and then uniformly sample from within that bin. So $p(u, v)$ is a conditional density on $p_{X}(x)$ the PDF to randomly select a bin, since we first draw a random variable to select a bin and then use it to sample from within it. As the events associated to the random variables $U$ and $V$ are independent (the incidence of one event does not affect the probability of the other event) we can also split the joint PDF: $p(u, v)=\frac{p_{U}(u)p_{V}(v)}{p_{X}(x)}$.
As $p_{U}(u)$, $p_{V}(v)$ and $p_{X}(x)$ are uniformly distributed (we generate random values using a uniform distribution with RandomFloat01()), we can write each of these PDFs as one over their domain: $p_{U}(u)=\frac{w_{env}}{w_{bin}}$, $p_{V}(v)=\frac{h_{env}}{h_{bin}}$, $p_{X}(x)=\frac{1}{N_{bins}}$, where $w_{env}$, $w_{bin}$ and $h_{env}$, $h_{bin}$ are the environment width, height and the selected bin width, height respectively, and $N_{bins}$ is the total number of bins.
We get: $p(u, v)=\frac{A_{env}}{N_{bins}A_{bin}}$, where $A_{bin}$ is the area of the randomly chosen bin and $A_{env}$ is the environment map area.
Finally, we have: $p(x, y, z)=\frac{A_{env}}{N_{bins}A_{bin}sin(\theta)2\pi^2}$ as our PDF for a random direction $(x, y, z)$.
Results
Below are the results with 5000 samples using importance sampling and then using uniform sampling.


References
Update
2023-02-04: Sample code to split an HDR environment map into bins by @0beqz